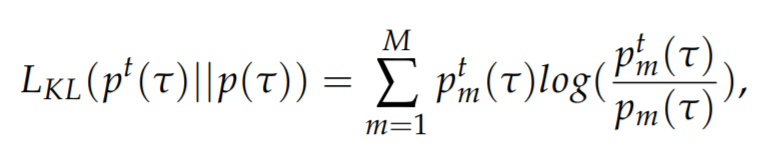Knowledge Distillation Part 1

1. Introduction

Knowledge Distillation is the process of transferring knowledge from a model to another model, usually a smaller one.

Supervised Machine learning relies on labels. Yet these labels provide limited signals. For example, in image recognition tasks, the labels are one-hot vectors with the entire probability assigned to the correct label; those labels do not provide any signal (information) about the incorrect labels. For example, An image of a cow is relatively similar to an image of a horse, but many times less similar to an image of a chair. This similarity structure is rich and valuable information and could be acquired from a teacher model and used to improve the training signal of a student model. Geoffrey Hinton calles this information Dark Knowledge.

To give you a human analog, when a kid mistakes a wasp for a bee or a rabbit for a gares parents don’t just say you’re wrong, but they often correct the kid and explain that they are similar but different animals. This similarity structure is missing from typical training data, but it can be acquired.

The training objective is to maximize the average log probability of the correct answer, but a side-effect of the learning process is that the model assigns probabilities to all classes (correct and incorrect). The relative probabilities of incorrect answers provide a missing similarity structure we talked about.

1.1. Where it used:

Knowledge Distillation is used in two main ways:

• Distilling to a smaller model (a model with less capacity): When building a smaller model for production use or to be used on mobile, knowledge distillation is often used to acquire more information from a bigger (expensive to productize) model. The student model is either trained to imitate the teacher model or to use the dark knowledge mentioned before as an enhanced training signal, or both.
• Distilling to same-size model: This approach is used to enhance the performance of a model where the teacher and student are the same size, in this case, the student usually uses the dark knowledge from a single or an ensemble of teachers.

2. Same size Knowledge Distillation:

There are two use-case for same-size knowledge distillation, either distilling from a small model to another small model or distilling from large model to another large model. Both are not very common because distilling from large to small typically works better than small to small (if you have a large model) and because once you have a large model that is usually sufficient. But I disagree. I believe that using this dark knowledge is very valuable to be ignored.

We know that an ensemble of models has better performance than a single model, in the same size knowledge distillation the aim is to try to improve the single model performance by acquiring the dark knowledge from an ensemble of models.

This form of distillation usually works using the logits. It starts with training the teacher model(s). Then during student model training, we compute soft targets from the teachers model logits using softmax function but with high temperature (T). (if we are using more than one model we average the logits before computing the soft-targets).

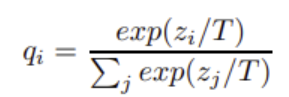
When the T term in the softmax is equal to 1, it’s the normal softmax. When it is bigger than 1, the distribution of the probabilities becomes softer. In general soft targets have the potential of working as a regularizer by reducing the model from being overconfident.

The objective (loss function) using to train the student is weight sum of two terms:

1. Knowledge Distillation Loss (LKL): The Kullback–Leibler divergence between the teacher output probability distribution and the student output probability distribution, both computed by the high temperature softmax mentioned above. Pt(t) is the teacher output distribution, P(t) is the student output distribution

2. Regular Loss: for example cross-entropy, typically without high temperature.

The alpha is the way to weight the losses. It controls how much we want the student model to imitate the teacher and how much we want the student to follow the regular cross-entropy loss.

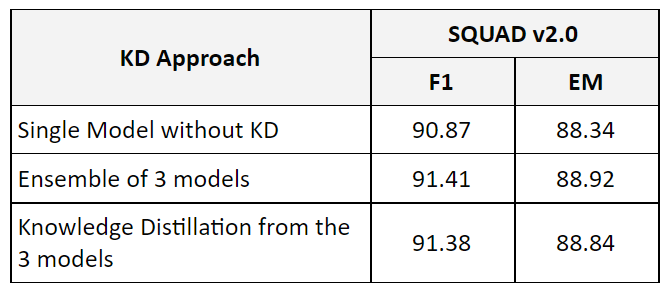
We applied Knowledge Distillation to ELECTRA-Large with MTL pre-training on SQUAD v2.0 dataset, here are the results:

4. Can we exceed the teacher performance

Those results are as expected. Same-size knowledge distillation improves the model performance significantly but it can’t match or exceed the teachers performance. This is one of the known limitations of same-size knowledge distillation. The student is limited by the teacher’s performance: The intuitive is simple, since the student is learned to imitate the teacher’s logits including the teacher’s mistakes it is bound by teacher performance and can’t do better.

We experimented with an approach called Teacher Annealing, in which the student early on tries to imitate the teacher then toward the end the student mostly relies on the gold-standard labels so it can learn to surpass its teachers. While this approach seems to be very promising and worth investigating further, we weren’t able to improve upon the typical KD after several experiments. We also experimented with iterative KD aka born-again-networks (Furlanello et al., 2018) in which we train a model, then use it as a teacher for a student model, then use the student model as a teacher for another model and so on but we weren’t able to surpass the typical KD.

5. KD with Improved Signal

Using first principle thinking, the value of Knowledge Distillation is the dark knowledge, the label with improved signal, but teachers make mistakes! So instead of procedure to control when the student learn from the teacher (such a in Teacher Annealing) we turned our attention the core of the problem ‘How to improve the teacher signal’ after several experiments we come up with Weighted Knowledge Distillation, which scale the logits according to the signal quality (correctness).

Weighted Knowledge Distillation scales the logits of the incorrect teachers by hyperparameter W < 1 (typically 0.75) and distributes the remaining weight to the correct teachers. The final weighting is computed such that to preserve the logits average value range. This way the student can focus on the information from the correct teachers. Here is the procedure to compute logits from M models

We compared the different knowledge distillation approaches. Here are the results:

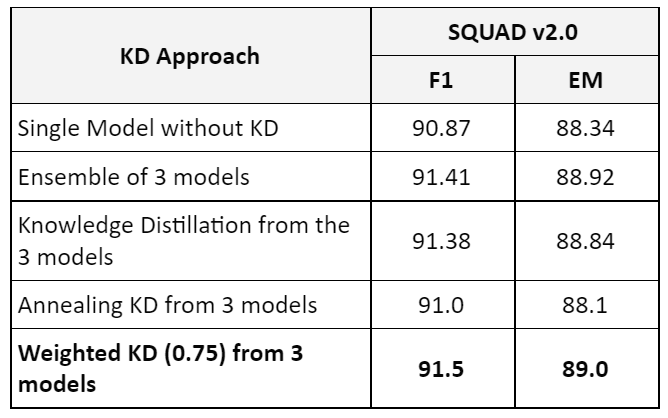
Weighted Knowledge Distillation is simple yet powerful way to improve the training signal, it allows the student model to exceed their teacher performance.