Decoupled Transformer

1. Introduction

Transformer models (e.g. BERT, RoBERTa, ELECTRA) have revolutionized the natural language processing space. Since its introduction there have been many new state-of-the-art results in MRC, NLI, NLU and machine translation. Yet Transformer models are very computationally expensive. There are three major factors that make Transformers models (encoders) expensive:

1. The size of the feed-forward layers which expand, activate then compress the representation.
2. The attention layer, while transformer avoids the sequential nature of RNNl it’s prohibitively expensive for long sequences because of its quadratic nature.
3. The number of layers.

There have been many ideas to make Transformers more performant, such as: Precision Reduction (Quantization), Distilling to a smaller architecture and Approximate Attention.

Here, we investigate another approach that is perpendicular to all other approaches (which means it can work alongside them). We call this approach Decoupled Transformer. Which decouple the inputs to improve efficiency.

2. Decoupled Transformer:

The idea of Decoupled Transformer is inspired by two things:

1. The fact that we can give humans a set of passages, then a question and the human will be able to answer the question from the passages.
2. In Transformer we concatenate the input (e.g. question and passage) and run them together through all the layers, But how much cross-attention (attention between the inputs, e.g. question and passage) is really needed?

In tasks where part of the transformer inputs doesn’t change often or could be cached, such as: Document Ranking in Information Retrieval (where the documents don’t change often), Question Answering (aka MRC) (where the passages don’t change often), Natural Language Inference Similarity matching, etc.

The decoupled transformer aims to reduce the inference efficiency by processing the inputs independently for part of the process and eliminating redundant computation, then process the inputs jointly for the later part of the proces.

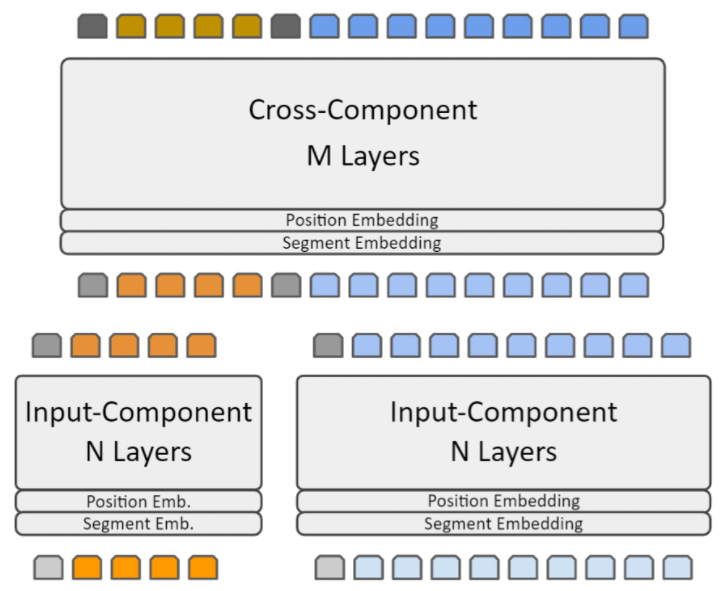
Decoupled transformer splits the transformer model into two components, an Input-Component (the lower N layers) which processes the inputs independently and produce a representation, which is cached and reused; and the Cross-Component (the higher M layers) which processes the inputs jointly (after concatenation) and produces the final output.

2.1. Decoupled Transformer Workflow in QnA

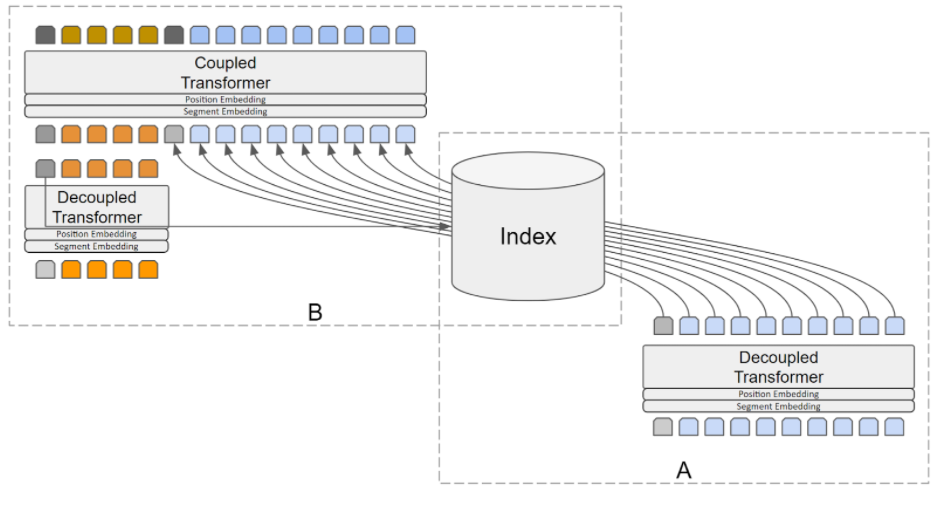
In information retrieval, question answering or similar use cases, we run the Input-Component part of the model on each document/passage while indexing the corpus and store the representation with the document/passage record (A in the image).

During inference (search or answering) we compute the query/question representation using the Input-Component part of the model as well, then we retrieve the candidate documents/passages with their representation from the index/DB, then we concatenate the query/question representation with the retrieved document/passage representation and run them though the Cross-Component part of the model. Figure 2 shows the workflow of the decoupled transformer in information retrieval/question answering scenario (B in the image).

2.2. Benefits and Cost

Benefits:

• Reduce the effective inference computation by caching and reusing the presentation of the long expensive part of the input, which is the document/passage - which is significantly longer than the query/question.
• Eliminate the redundant query/question representation computation which happens in the typical method of processing.

Cost:

• Decoupled Transformer requires storing the document/passage representation which could be significant, but we will discuss ways to reduce it.

3. Experiments

3.1 Creating Decoupled Transformer

We start from a fine-tuned model, then we create the decoupled model by splitting the encoder layers into Input-Component and Cross-Component, note we keep the learned weight unchanged. We also create a position embedding and segment embedding layers at the start of the Cross-Component and initialize them to the same weights as the position and segment embedding from the decoupled part.

Starting from a pre-trained model is possible but in our experiments it didn’t perform as well compared to starting from a fine-tuned model.

3.2 Training Procedure

Our goal is to preserve the model performance, so we opted to use knowledge distillation from the original model in the finetuning process to help the model imitate the behavior and learn their representation.

The loss function is the sum of three terms:

1. The logits loss with knowledge distillation using (Hinton et al., 2015) formulation which is a weighted average of two objectives. The first objective is the original cross entropy with correct labels. The second objective is the Kullback–Leibler divergence with the soft targets from the teacher. For the soft targets in the second objective we use the same high temperature in the softmax of the teacher and student model.
2. Mean square error between the decoupled model final layer hidden representation with the original model final layer hidden representation.
3. Mean square error between the decoupled model final layer self-attention representation with the original model final layer self-attention representation.

This training procedure inspired by TinyBERT except that we only apply the feature derived losses (hidden representation and self-attention) to the last layer only and we scale it by 0.5

3.3 Experiments and Results

One of the big questions we were trying to answer is, How much cross-attention (between the inputs) is really needed? We evaluated our approach on a diverse set of datasets. We used SQUAD 2.0 (Machine Reading Comprehension), QQP and MRPC (paraphrasing identification) and MNLI (natural language Inference). We used ELECTRA-Base for all the datasets, except for SQUAD 2.0 we used ROaD-Base which is the current state of the art model for SQUAD 2.0 and is based on ELECTRA architecture as well.

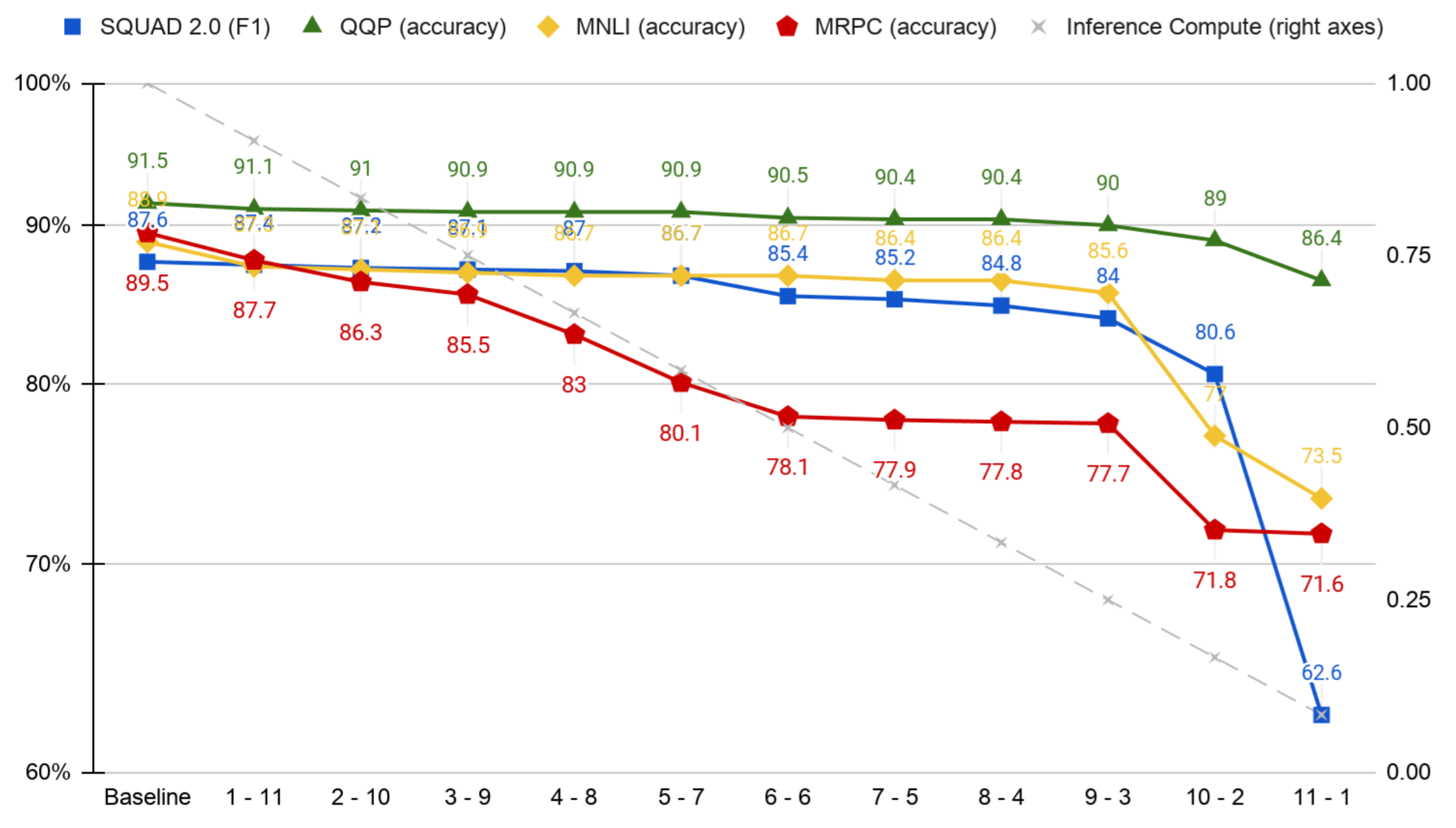
This figure shows the performance starting from the baseline (without decoupling, 0-12) to decoupling with 11 layers in the Input-Component part, and 1 in the Cross-Component part. We observed that tasks with a big dataset have similar behavior with noticeable drop when moving from 5 layers input-component - 7 layers cross–component to 6 layers input-component - 6 layers cross-component and another big drop when the number of cross-component layers becomes less than 3. While MRPC had similar characteristics the drop of performance was significant overall.

4. Compression

In the decoupled transformer we need to cache the representation produced by the decoupled transformer for one of the inputs, which could be a significant amount of storage. In case of question answering over Wikipedia where we cache the passage representation, this could be 6.8TB assuming (32 million passage, 150 token per passage, 768 token dimension for base BERT model, float16).

6.8TB could be a significant amount of storage, therefore we introduced a compression layer at the end of the Input-Component model and decompression layer at the start of the Cross-Component model, similar to autoencoders. The additional layer is a linear projection layer that projects the input to another (smaller or larger) dimension.

4.1. Training Procedure

We start from a regular fine-tuned model, decoupe it as in the previous experiment and add the compression/decompression layers. We perform the finetuning in 2 phases. In the first phase we optimize the compression/decompression layer independent of the rest of the model, which means the cross-component part receives the representation without modification (without compression/decompression). In the second phase, we optimize everything jointly, which means the cross-component part receives the decompressed representation. The intuition behind this approach is that the model is already initialized (pre-trained and fine-tuned) while the compression/decompression layers aren’t so we first need to train those layers independent from the model and then use the decompressed representation to tune the coupled part of the model to understand the slightly different representation.

4.2. Experiments and Results

We applied the compression approach on a 5 Input / 7 Cross MRC model on SQUAD 2.0 dataset to investigate how much impact does the different levels of compression have on the model performance.

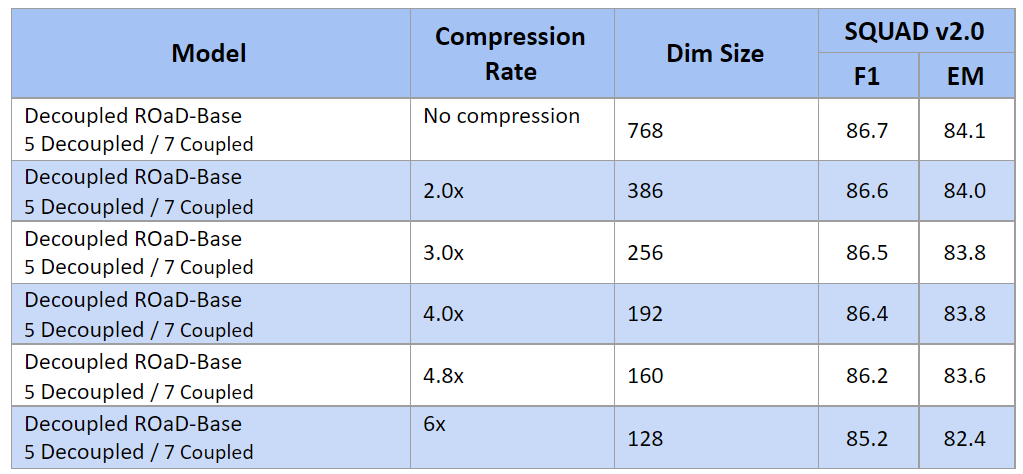
We observed the performance degradation is minimal for 2x, 3x and 4x compression and then it started to accelerate.

At 4x compression the required storage for Question answering over Wikipedia with the previous assumptions is 1.7TB which could be reduced 850GB if we used INT8

5. Final Model

Our final decoupled model named: Decoupled ROaD-Base model with 4x compression is not just very efficient but perform better than other state-of-the-art models (e.g. DeBERTa, ELECTRA)